Sudoku Checker

Sudoku is one of the popular logic-based puzzle games. It consists of a partially-filled 9x9 grid of numbers between 1 to 9 and the objective of the puzzle is to fill in the missing numbers in a way such that every row, every column, and every inner square contains all numbers from 1 to 9 appearing exactly once. A solved state of the Sudoku looks something like this:

Notice that every row has every number from 1 to 9 exactly once:

Similarly, every column has every number from 1 to 9 exactly once:

Finally, every inner square has every number from 1 to 9 exactly once:

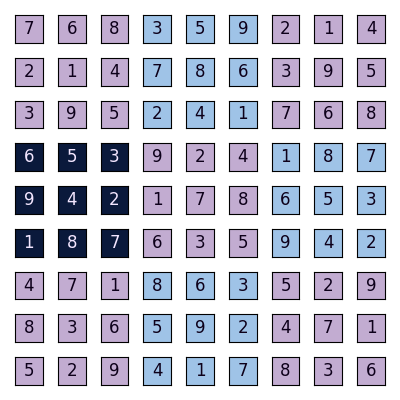
This makes it a valid Sudoku. A Sudoku is invalid if there are any duplicate numbers along any row, column, or inner square.

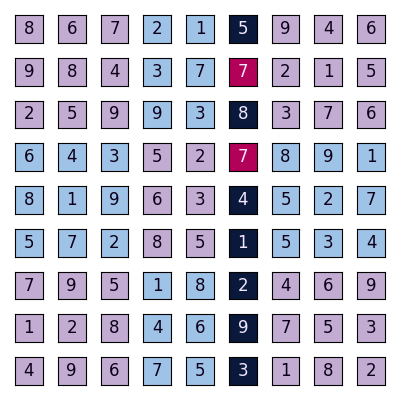
The following is an invalid Sudoku:

Note that 9 appears twice in the seventh row, making this row invalid:

7 appears twice in the sixth column, making this column invalid:

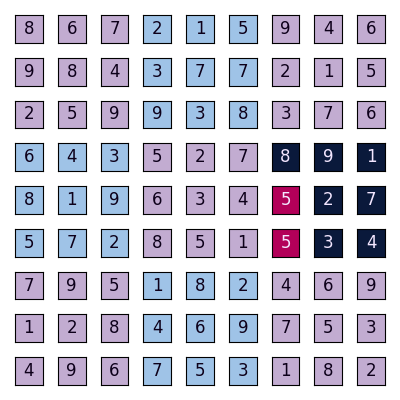
Finally, 5 appears twice inside the sixth inner square (counting from left to right, top to bottom), making this inner square invalid:

Exercise

Write a program using NumPy that takes in a 2D array sudoku and returns three arrays in the following order:

• rows_valid: 9-element boolean array representing which rows are valid and which are not
• columns_valid: 9-element boolean array representing which columns are valid and which are not
• squares_valid: 9-element boolean array representing which inner squares are valid and which are not

Sample Test Cases

Test Case 1

Input:

[
  [[7, 6, 8, 3, 5, 9, 2, 1, 4],
   [2, 1, 4, 7, 8, 6, 3, 9, 5],
   [3, 9, 5, 2, 4, 1, 7, 6, 8],
   [6, 5, 3, 9, 2, 4, 1, 8, 7],
   [9, 4, 2, 1, 7, 8, 6, 5, 3],
   [1, 8, 7, 6, 3, 5, 9, 4, 2],
   [4, 7, 1, 8, 6, 3, 5, 2, 9],
   [8, 3, 6, 5, 9, 2, 4, 7, 1],
   [5, 2, 9, 4, 1, 7, 8, 3, 6]]
]

Output:

rows_valid = [True, True, True, True, True, True, True, True, True]
columns_valid = [True, True, True, True, True, True, True, True, True]
squares_valid = [True, True, True, True, True, True, True, True, True]

Test Case 2

Input:

[
  [[8, 6, 7, 2, 1, 5, 9, 4, 6],
   [9, 8, 4, 3, 7, 7, 2, 1, 5],
   [2, 5, 9, 9, 3, 8, 3, 7, 6],
   [6, 4, 3, 5, 2, 7, 8, 9, 1],
   [8, 1, 9, 6, 3, 4, 5, 2, 7],
   [5, 7, 2, 8, 5, 1, 5, 3, 4],
   [7, 9, 5, 1, 8, 2, 4, 6, 9],
   [1, 2, 8, 4, 6, 9, 7, 5, 3],
   [4, 9, 6, 7, 5, 3, 1, 8, 2]]
]

Output:

rows_valid = [False, False, False, True, True, False, False, True, True]
columns_valid = [False, False, False, True, False, False, False, True, False]
squares_valid = [False, False, False, True, False, False, False, True, True]