Riemann Sums

A Riemann sum, one of the many things named after Bernhard Riemann, is a finite sum that can be used to approximate an integral by partitioning the area under a curve into rectangles. This problem will explore the process of approximating area under a curve using Riemann sums.

Definition

Consider the following function:

We need the area under this function between and . In other words, we need to approximate the following integral:

We can plot the function to get a better idea of what it looks like:

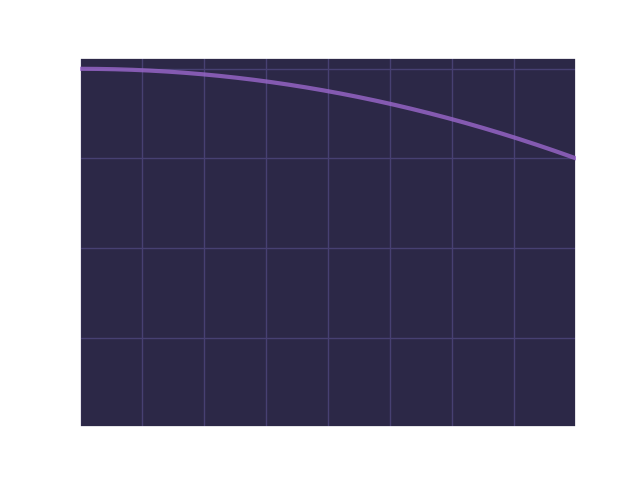
If we manually compute the definite integral, we get recurring. Let's see how good our approximations are!

Left Riemann Sum

We can partition this function into 4 evenly spaced sections of width 0.5 and draw rectangles such that the top-left corner of the rectangle touches the function's curve:

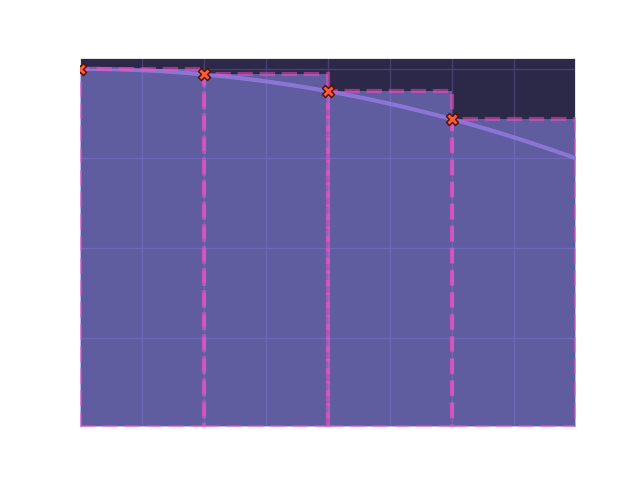
Now all we need to do is find the total area of all these rectangles:

Close! But we overshot. Can we do better?

Right Riemann Sum

Now we can draw rectangles such that the top-right corner of the rectangle touches the function's curve:

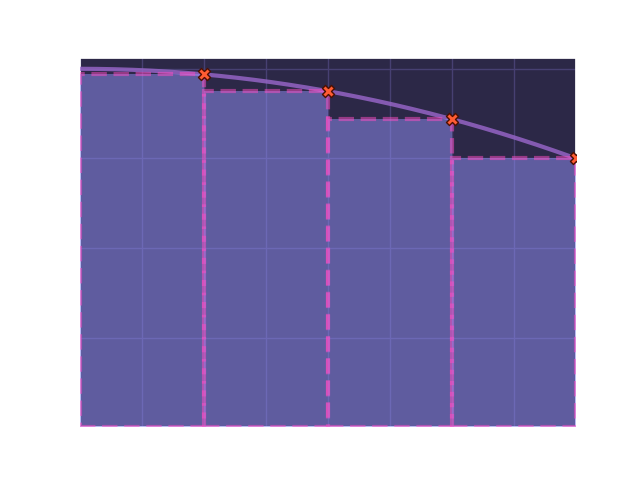
Once again, we need to do is find the total area of all these rectangles:

Close again! But this time we undershot. Let's try one more time.

Mid-point Riemann Sum

We can draw rectangles such that the mid-point of the rectangle's top touches the function's curve:

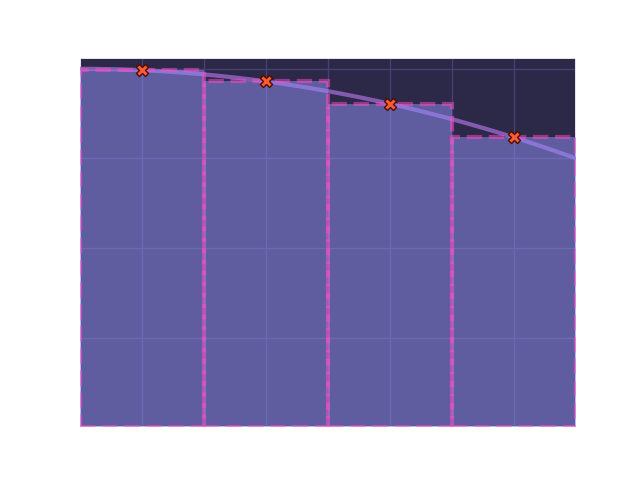
Finally, we need to do is find the total area of all these rectangles:

That's our best approximation so far!

Exercise

Write a program using NumPy that approximates the area under a curve using Rieman sums. Complete the compute_left_riemann_sum(), compute_right_riemann_sum(), and compute_midpoint_riemann_sum() methods:

• compute_left_riemann_sum() takes in a function f, a pair of limits limits, and the number of partitions n, and computes the Riemann sum using rectangles that touch the curve using their top-left corners
• compute_right_riemann_sum() takes in a function f, a pair of limits limits, and the number of partitions n, and computes the Riemann sum using rectangles that touch the curve using their top-right corners
• compute_midpoint_riemann_sum() takes in a function f, a pair of limits limits, and the number of partitions n, and computes the Riemann sum using rectangles that touch the curve using the mid-point of their tops

Sample Test Cases

Test Case 1

Input:

[
  [-1, 0, 16],
  [0, 2],
  4
]

Output:

left_riemann_sum = 30.25
right_riemann_sum = 28.25
midpoint_riemann_sum = 29.375

Test Case 2

Input:

[
  [1,3,2],
  [-2, 2],
  4
]

Output:

left_riemann_sum = 8.0
right_riemann_sum = 20.0
midpoint_riemann_sum = 13.0