K-Nearest Neighbours

One of the simplest supervised, non-parametric machine learning classification algorithms is known as the K-Nearest Neighbours algorithm. For this exercise, we will explore and implement KNN.

Definition

In KNN classification, we are given a set of feature vector-target pairs:

What does this mean? This tells us that when the feature vector is , our target class is .

Now suppose we are given a new feature vector and want to predict the target class . How do we go about this? Before we answer that, we can compute a set of distances that consists of the Euclidean distances between and every point in :

Once we have the distances, the idea is to obtain the -closest neighbours of by picking the -lowest distances in , and note down their corresponding target classes. Among the target classes, we choose the most frequently occurring one to be .

For example, consider a subset of the Iris dataset from the UCI Machine Learning Repository that includes data on different species of the Iris plant:

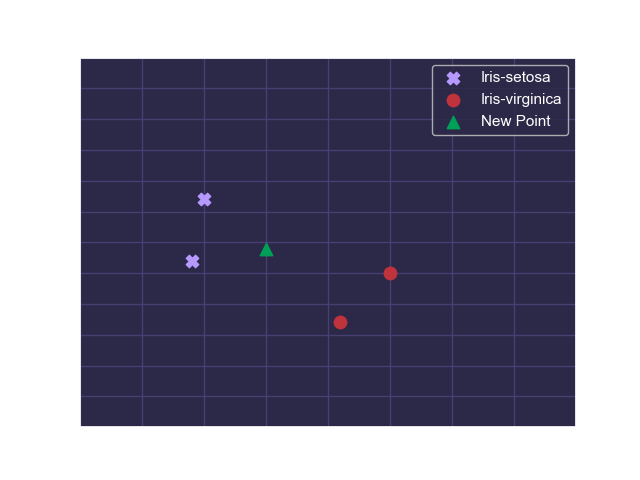
We know the blue points to be of class Iris-setosa and the red points to be of class Iris-virginica. But the green point is of an unknown class and must be classified. We can identify the top 3 nearest neighbours to the green point:

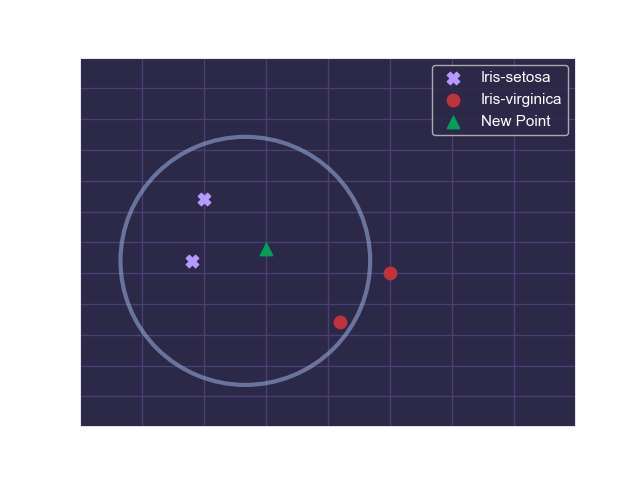
As we can see, out of the 3 nearest neighbours, 2 of them are of class Iris-setosa and 1 of them is of class Iris-virginica. Since Iris-setosa occurs more frequently than Iris-virginica, we choose Iris-setosa as the predicted target class .

Performance Metric

We also need a performance metric to determine how good our classification is. To this end, we can simply use the accuracy of our prediction. Before we define the accuracy of prediction, we must define a few other terms:

	Actually 1	Actually 0
Predicted 1	True Positive	False Positive
Predicted 0	False Negative	True Negative

• True Positives are data points that are 1s and have been successfully predicted to be 1s
• False Positives are data points that are 0s but have been erroneously predicted to be 1s
• False Negatives are data points that are 1s and have been erroneously predicted to be 0s
• True Positives are data points that are 0s and have been successfully predicted to be 0s

We define our accuracy metric to be the fraction of data points that have been identified correctly. In other words:

where , , , and are the number of true positives, true negatives, false positives, and false negatives respectively in our prediction.

In the case of this exercise, the accuracy metric can be defined as follows:

where is the number of points such that the predicted is equal to the actual , and is the number of points such that the predicted is not equal to the actual . This will yield a value between 0 and 1 indicating how good our prediction is.

Exercise

Write a program that performs KNN classification. Complete the predict(), and score() methods:

• fit() takes in arrays X and y, and stores this data (this function was already written for you)
• predict() takes in array X and number of neighbours k, and returns a predicted array y_pred by performing KNN using the stored data
• score() takes in arrays X and y and number of neighbours k, predicts the y_pred values using X and the stored data, and then uses y_pred and y arrays to compute and return the accuracy of prediction

You may assume there will be no ties between distances or target class frequencies.

Sample Test Cases

Test Case 1

Input:

[
  [[5,   3.6],
   [6.1, 2.6],
   [6.5, 3  ],
   [4.9, 3.1]],
   [0, 1, 1, 0],
  [[5.5, 3.2]],
   [0],
    2
]

Output:

y_pred = [0]
accuracy = 1.0

Test Case 2

Input:

[
  [[4.1, 0.2],
   [5.2, 0.8],
   [1.9, 2.2],
   [2,   1.4],
   [6.8, 0  ],
   [1.2, 3  ],
   [0.3, 2.4],
   [6.8, 0.8],
   [0.9, 0.1],
   [4.8, 2.1]],
   [0, 0, 1, 0, 0, 1, 1, 1, 1, 0],
  [[2,   2.8],
   [5.9, 1.1]],
   [0, 0],
    3
]

Output:

y_pred = [1, 0]
accuracy = 0.5