Activation Functions

One of the most crucial roles in neural network architecture is played by activation functions. Activation functions are simple transformations that are applied to the outputs of individual neurons in the network, introducing non-linearity to it and enabling it to learn more complex patterns. For this exercise, we will explore and implement different types of activation functions.

An activation function takes in an matrix of values and transforms it into . Note that the sizes of matrices and are the same.

In this exercise, we will explore 5 of the most common activation functions.

Step Function

The step function is defined by:

The following is a plot of the step function:

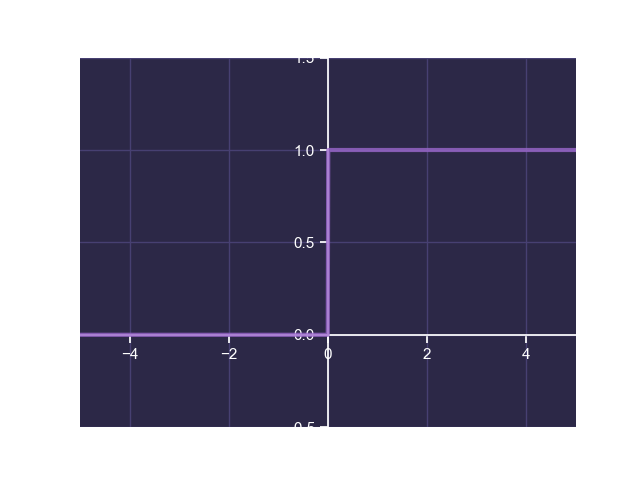
The step function transforms a continuous input to a binary output and is often used as the final layer in a binary classification network. However, because it's derivative is undefined at and is equal to everywhere else, it is not very useful for learning in neural networks.

Sigmoid Function

The sigmoid function is defined by:

The following is a plot of the sigmoid function:

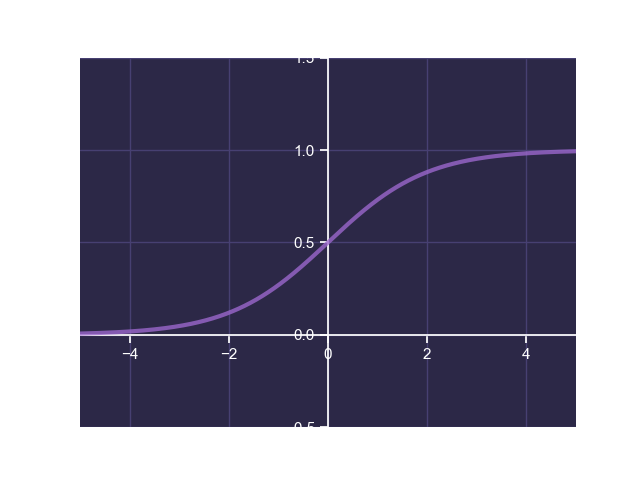
The sigmoid function transforms a continuous input to a continuous output between 0 and 1. This property is extremely useful for neural networks tasked with classification. Additionally, the sigmoid function is differentiable for all values of , making it suitable for learning algorithms.

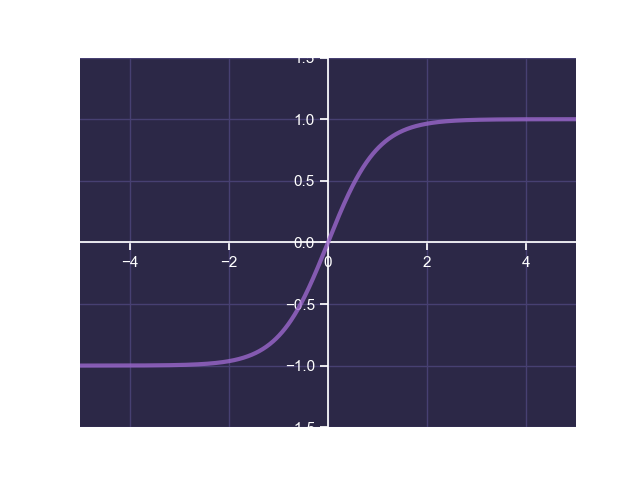
Hyperbolic Tangent

The hyperbolic tangent is defined by:

The following is a plot of hyperbolic tangent:

Hyperbolic tangent transforms a continuous input to a continuous output between -1 and 1. Once again this is useful for neural networks tasked with classification. Like the sigmoid function, the hyperbolic tangent is also differentiable for all values of , making it suitable for learning algorithms.

Rectified Linear Unit

The rectified linear unit (ReLU) function is defined by:

The following is a plot of ReLU:

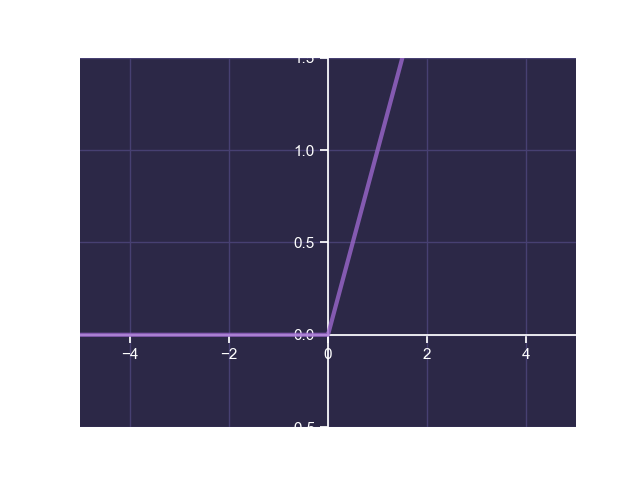
ReLU transforms a continuous input to a continuous positive output. It is also useful for neural networks and can often be used to avoid the vanishing gradient problem observed with the sigmoid function.

Leaky Rectified Linear Unit

The leaky rectified linear unit function is defined by:

The following is a plot of leaky ReLU:

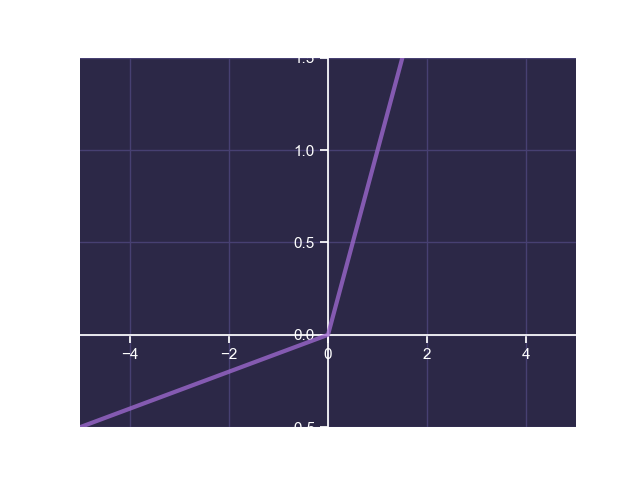
Leaky ReLU transforms a continuous input to a continuous output, where the gradient of the output when the input is negative is given by the parameter . Unlike ReLU, leaky ReLU does not output when the input is zero. This helps avoid the dying ReLU problem that is often observed with ReLU.

Softmax

The entry of the softmax function's output is defined as follows:

where is the entry of matrix .

The following is a visualization of how softmax works:

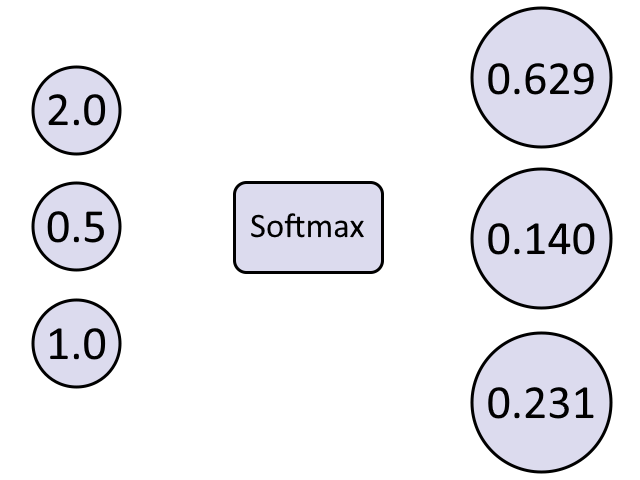
Note that the softmax function is the only one in this exercise that cannot be applied individually to each element in and must be applied collectively to all the elements in . Softmax transforms a set of continuous input values to a set of corresponding continuous probability values between 0 and 1. This is often useful for neural networks in multi-class classification problems.

Exercise

Write a program using NumPy that performs the activation functions on a given input. Complete the sigmoid(), tanh(), relu(), leaky_relu(), and softmax() methods:

• step() takes in a multi-dimensional input array X, performs the step function on each element and returns the result as an array of the same shape. This has already been implemented for you.
• sigmoid() takes in a multi-dimensional input array X, performs the sigmoid function on each element and returns the result as an array of the same shape
• tanh() takes in a multi-dimensional input array X, performs the hyperbolic tangent function on each element and returns the result as an array of the same shape
• relu() takes in a multi-dimensional input array X, performs ReLU on each element and returns the result as an array of the same shape
• leaky_relu() takes in a multi-dimensional input array X, performs leaky ReLU on each element and returns the result as an array of the same shape
• softmax() takes in a multi-dimensional input array X, performs the softmax function and returns the result as an array of the same shape

Sample Test Cases

Test Case 1

Input:

[
  [2, 0.5, 1],
  0.25
]

Output:

sigmoid = [0.881, 0.622, 0.731]
tanh = [0.964, 0.462, 0.762]
relu = [2, 0.5, 1]
leaky_relu = [2, 0.5, 1]
softmax = [0.629, 0.14, 0.231]

Test Case 2

Input:

[
  [-1, 2],
  0.1
]

Output:

sigmoid = [0.269, 0.881]
tanh = [-0.762, 0.964]
relu = [0, 2]
leaky_relu = [-0.1, 2]
softmax = [0.047, 0.953]